Twelve Days 2013: De Bruijn Sequences

Day Ten: De Bruijn Sequences

TL/DR

De Bruijn sequences and more generally De Bruijn graphs have lots of cool applications in combinatorics and CS. On hardware lacking a native instruction to count leading zeros in a word or find the least significant bit, a perfect hash function formed using a De Bruijn sequence provides a constant time solution. The technique is still useful when implementing arbitrary length integers or bit vectors. Outside of bit twiddling, De Bruijn graphs, sequences, and arrays improve the precision of encoders used in robotics and digital tablets, contribute to DNA fragment analysis, and find use in cryptographic applications.

Intro to De Bruijn Graphs

De Bruijn graphs are Eulerian, Hamiltonian digraphs with a few special properties. if we have an alphabet $\Sigma$ with $m$ symbols, the graph will have $m^n$ vertices, where $n$ is a free parameter. The vertex set is constructed such that every $n$ character word formed by characters taken from the alphabet is represented by a single vertex. The edge set is constructed in a fashion that encodes "overlap" between the words. De Bruijn sequences are the Hamiltonian cycles of the graph.

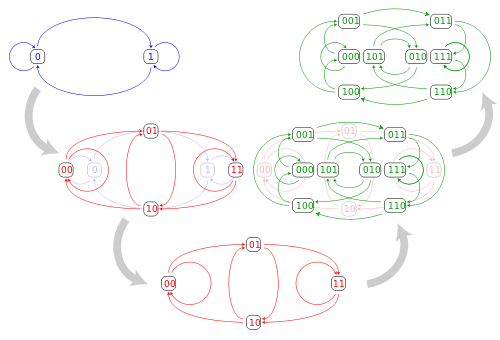
DeBruijn Digraph

Why De Bruijn Sequences are Interesting

Under the construction above, De Bruijn sequences have the property that every $n$ character word in a $k$ character alphabet appears as a sub sequence exactly once when we slide a $n$ character window along the sequence from left to right. As an example, one construction of $B(2, 3)$ is $\{0, 0, 0, 1, 0, 1, 1, 1\}$ . As we slide a three element long window from left to right, wrapping around when necessary we get:

\begin{aligned} 000 & = 0 \\ 001 & = 1 \\ 010 &= 2 \\ 101 &= 5 \\ 011 &= 3 \\ 111 &= 7 \\ 110 &= 6 \\ 100 &= 4 \end{aligned}

Every number in the range $[0, 7]$ appears exactly once. For a binary alphabet the length of the sequence will always be $2^n$ but for larger alphabets the sequence can be shorter than direct enumeration. As wikipedia points out, this has the useful property that, given a lock that accepts a pin code without an enter key (which was apparently common in Europe at one point), entering a De Bruijn sequence for the appropriate alphabet and code length is the fastest way to crack the lock. For a ten digit entry pad and a four digit pin that amounts to $B(10, 4)$ , which is 10,000 characters long. Compare that with the $4 * 10^4 = 40,000$ combinations that would be required otherwise.

The ability of De Bruijn graphs/sequences to efficiently encode overlap makes them useful for things like DNA sequencing where overlapping fragments need to be recombined, and for mechanical/optical encoders that need to figure out where they are given some overlapping sequence of measurements. There's also a neat bit twiddling hack that comes about from this which we'll discuss next.

De Bruijn Sequences and Minimal Perfect Hashes

A perfect hash is an injective map $S \mapsto \mathbb{Z}$ : a function that maps all elements of $S$ onto the integers with no collisions. Minimal perfect hash functions have the additional property that keys are mapped to integers consecutively. By a simple cardinality argument that also implies that the function is as "efficient" as possible. There's a seminal paper discussing how De Bruijn sequences can be used to construct a minimal perfect hash function that, given any integer $i$ , will return the location of the lowest (rightmost) set bit in $i$ . This is a pretty common and important operation to the extent that lots of processors now offer an instruction to do this. However, if you look at the code behind a compiler intrinsic that performs the find-first-set operation, the fallback for architectures lacking native support usually involves this hack.

Before going any further it's worth noting that, if you've heard of this hack, you've probably also seen magic De Bruijn constant floating around for integers of various length. De Bruijn sequences are not necessarily unique and they depend on the algorithm used to generate them. Don't be surprised if the constants that you've seen don't match the ones generated by this code.

DeBruijn.java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
import java.util.Random;

/**
 * @author Kelly Littlepage
 */
public class DeBruijn {

    /***
     * Generate a De Bruijn Sequence using the recursive FKM algorithm as given
     * in http://www.1stworks.com/ref/RuskeyCombGen.pdf .
     *
     * @param k The number of (integer) symbols in the alphabet.
     * @param n The length of the words in the sequence.
     *
     * @return A De Bruijn sequence B(k, n).
     */
    private static String generateDeBruijnSequence(int k, int n) {
        final int[] a = new int[k * n];
        final StringBuilder sb = new StringBuilder();
        generateDeBruijnSequence(a, sb, 1, 1, k, n);
        return sb.toString();
    }

    private static void generateDeBruijnSequence(int[] a,
                                                 StringBuilder sequence,
                                                 int t,
                                                 int p,
                                                 int k,
                                                 int n) {
        if(t > n) {
            if(0 == n % p) {
                for(int j = 1; j <= p; ++j) {
                    sequence.append(a[j]);
                }
            }
        } else {
            a[t] = a[t - p];
            generateDeBruijnSequence(a, sequence, t + 1, p, k, n);
            for(int j = a[t - p] + 1; j < k; ++j) {
                a[t] = j;
                generateDeBruijnSequence(a, sequence, t + 1, t, k, n);
            }
        }
    }

    /***
     * Build the minimal perfect hash table required by the De Bruijn ffs
     * procedure. See http://supertech.csail.mit.edu/papers/debruijn.pdf.
     *
     * @param deBruijnConstant The De Bruijn number to use, as produced by
     * {@link DeBruijn#generateDeBruijnSequence(int, int)} with k = 2.
     * @param n The length of the integer word that will be used for lookup,
     * in bits. N must be a positive power of two.
     *
     * @return A minimal perfect hash table for use with the
     * {@link DeBruijn#ffs(int, int[], int)} function.
     */
    private static int[] buildDeBruijnHashTable(int deBruijnConstant, int n) {
        if(!isPositivePowerOfTwo(n)) {
            throw new IllegalArgumentException("n must be a positive power " +
                    "of two.");
        }
        // We know that n is a power of two so this (meta circular) hack will
        // give us lg(n).
        final int lgn = Integer.numberOfTrailingZeros(n);
        final int[] table = new int[n];
        for(int i = 0; i < n; ++i) {
            table[(deBruijnConstant << i) >>> (n - lgn)] = i;
        }
        return table;
    }

    /***
     * Tests that an integer is a positive, non-zero power of two.
     *
     * @param x The integer to test.
     * @return <code>true</code> if the integer is a power of two, and
     * <code>false otherwise</code>.
     */
    private static boolean isPositivePowerOfTwo(int x) {
        return x > 0 && ((x & -x) == x);
    }

    /***
     * A find-first-set bit procedure based off of De Bruijn minimal perfect
     * hashing. See http://supertech.csail.mit.edu/papers/debruijn.pdf.
     *
     * @param deBruijnConstant The De Bruijn constant used in the construction
     * of the deBruijnHashTable.
     * @param deBruijnHashTable A hash 32-bit integer hash table, as produced by
     * a call to {@link DeBruijn#buildDeBruijnHashTable(int, int)} with n = 32.
     * @param x The number for which the first set bit is desired.
     *
     * @return <code>32</code> if x == 0, and the position (in bits) of the
     * first (rightmost) set bit in the integer x. This function chooses to
     * return 32 in the event that no bit is set so that behavior is consistent
     * with {@link Integer.numberOfTrailingZeros()}.
     */
    private static int ffs(int deBruijnConstant,
                           int[] deBruijnHashTable, int x) {
        if(x == 0) {
            return 32;
        }
        x &= -x;
        x *= deBruijnConstant;
        x >>>= 27;
        return deBruijnHashTable[x];
    }


}

The code above will generate a De Bruijn sequence and the hash table necessary for the first-set-bit look-up. How does it stack up against the LZCNT instruction emitted by Hotspot on x86?