The Geometry of Signal Extraction
Teasing out the Signal
There’s a classic signal extraction problem stated as follows: you observe a random variable as the sum of two normal distributions, and such that . Given an observation of , what is the conditional expectation of ?
The problem asks us to find . There are a number of reasons why we might want to do so. For starters, if we’re interested in the value of some Gaussian distribution , but we can only observe , the conditional expectation given above is exactly what we’re looking for. In the past I’ve seen it derived hammer and tongs via the definition of conditional expectation:
If and are statistically independent we can express the joint distribution as a product of marginal distributions, fix , and end up with the expression that we’re looking for:
Ouch. It works, but it’s not pretty. Last night I came up with a geometric interpretation for the normal case that I wanted to share. Googling around there are similar derivations but I figured that one more writeup with some deeper explanation wouldn’t hurt.
Regression as an Operator
To start we note a general propriety of conditional expectation: , where is some measurable function. We also need a simple decomposition lemma: any random variable can be written as: , where is a RV s.t. and . The intuition here is that almost by definition any variable can be expressed as a conditional expectation and an error term. The proof is simple:
We need this to prove the following result:
Proof:
From the decomposition property that we proved above so the second term simplifies to . Now let in expectation by the second decomposition property. Thus, we’re left with the first term (not a function of , and the third term, which vanishes when , thus minimizing the function. QED.
A Geometric Interpretation
If the joint distribution of and is normal (and it is for for our example—the joint distribution of a sum of normal distributions is always normal, even if they’re not independent) . I won’t prove this as it’s repeated many times over in the derivation of linear regression. Why do we care? At the end of the day is just another random variable. We can set aside the fact that and note that is actually just regression. Our nasty integral formula for conditional expectation has a beautiful geometric interpretation: . We can work out our original signal extraction problem using the formula for simple linear regression:
and:
Applying this to our problem:
The fact that results from our earlier stipulation that the distributions are independent. We also have that:
Thus,
and:
Putting it all together and simplifying gives us our final form:
Note that when the means are zero the formula above becomes a simple ratio of variances. That’s a pretty satisfying result—when accounts for most of the variance it’s reasonable to expect that, when has a zero mean, the bulk of whatever we observe comes from variance in . This is very closely related to how principal component analysis works.
Visualizing the Result
Let’s start by taking a look at the density of our 2D Gaussian:
n <- 100000
mu_x <- 1
mu_y <- 2
sigma_x <- 1
sigma_y <- 2
x <- rnorm(n, mean = mu_x, sd = sigma_x)
y <- rnorm(n, mean = mu_y, sd = sigma_y)
var_z <- sigma_x^2 + sigma_y^2
beta <- sigma_x^2 / var_z
alpha <- mu_x - beta * (mu_x + mu_y)
df <- data.frame(x, y)
ggplot(df, aes(x = x, y = y)) +
stat_density2d(aes(fill = ..level..), geom="polygon") +
geom_abline(intercept = alpha, slope = beta, color = "red",
linetype = "longdash") +
geom_vline(xintercept = mu_x, color = "red", linetype = "dotted") +
geom_hline(yintercept = mu_y, color = "red", linetype = "dotted") +
theme(plot.background = element_rect(fill = '#F1F1F1'),
legend.background = element_rect(fill = '#F1F1F1')) +
ggtitle("2D Normal Density")
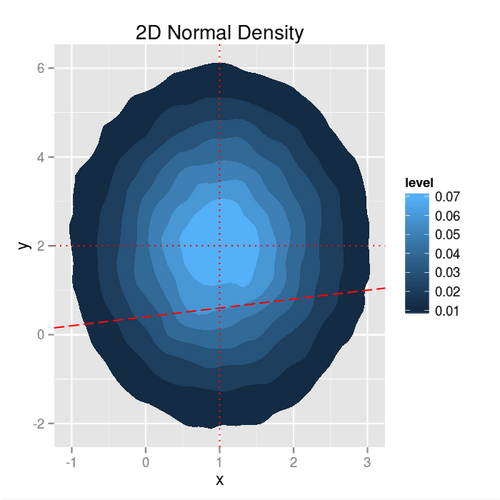
The density above resulted from the sum of two independent normal distributions and . As such, it’s centered at , and elongated along the axis. Plugging in the parameters of our distributions gives and . Fitting the simulation data we find that our equation holds:
summary(lm(x ~ z))
Call:
lm(formula = x ~ z)
Residuals:
Min 1Q Median 3Q Max
-3.5625 -0.6019 -0.0021 0.6016 3.9475
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.400942 0.004733 84.71 <2e-16 ***
z 0.199886 0.001263 158.29 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.8946 on 99998 degrees of freedom
Multiple R-squared: 0.2004, Adjusted R-squared: 0.2004
F-statistic: 2.506e+04 on 1 and 99998 DF, p-value: < 2.2e-16
Note that , the same as our value of . For a simple linear regression is simply the squared correlation coefficient, or in our case:
That gives us a cool new interpretation of as the proportion of variance explained. It does however hint at a shortcoming that has as a goodness of fit measure—it explicitly depends on how our regressors are distributed.
At this point we have a simple formula to calculate a very useful conditional expectation. We also have a nice geometric interpretation of the solution, and an understanding that both regression and our original signal extraction problem distill down to a ratio of variances. Fantastic. However, we’re assuming that we know the proper, fixed parametrization of our model: , and that’s pretty unlikely. How do we estimate these parameters for a time-variant system given that we can only observe a series of ? There are a myriad of approaches, each with pros, cons, and assumptions. Mixture models and machine learning are growing in favor for many applications. The CDS approach usually involves posing the model as a state space and estimating the parameters online. There’s no easy way out when faced with a partially observed, non-stationary process. So sorry folks—when it comes to denoising your signal, the equation above is the easy part.
