Measuring Randomness in Capital Markets
What is Random?
As previously discussed, there's no universal measure of randomness. Randomness implies the lack of pattern and the inability to predict future outcomes. However, The lack of an obvious model doesn't imply randomness anymore than a curve fit one implies order. So what actually constitutes randomness, how can we quantify it, and why do we care?
Randomness Volatility, and Predictability Profit
First off, it's important to note that predictability doesn't guarantee profit. On short timescales structure appears, and it's relatively easy to make short term predictions on the limit order book. However, these inefficiencies are often too small to capitalize on after taking into account commissions. Apparent arbitrage opportunities may persist for some time as the cost of removing the arb is larger than the payout.
Second, randomness and volatility are oft-used interchangeably in the same way that precision and accuracy receive the same colloquial treatment. Each means something on its own, and merits consideration as such. In the example above, predictability does not imply profitability anymore than that randomness precludes it. Take subprime for example – the fundamental breakdown in pricing and risk control resulted from correlation and structure, not the lack thereof.
Quantifying Randomness
Information theory addresses the big questions of what is information, and what are the fundamental limits on it. Within that scope, randomness plays an integral role in answering questions such as "how much information is contained in a system of two correlated, random variables?" A key concept within information theory is Shannon Entropy – a measure of how much uncertainty there is in the outcome of a random variable. As a simple example, when flipping a weighted coin, entropy is maximized when the probability of heads or tails is equal. If the probability of heads or tails is .9 and .1 respectively, the variable is still random, but guessing heads is a much better bet. Consequently, there's less entropy in the distribution of binary outcomes for a weighted coin flip than there is for a fair one. The uniform distribution is a so called maximum entropy probability distribution as there's no other continuous distribution with the same domain and more uncertainty. With the normal distribution you're reasonably sure that the next value won't be far away from the mean on one of the tails, but the uniform distribution contains no such information.
There's a deep connection between entropy and compressibility. Algorithms such as DEFLATE exploit patterns in data to compress the original file to a smaller size. Perfectly random strings aren't compressible, so is compressibility a measure of randomness? Kolmogorov complexity measures, informally speaking, the shortest algorithm necessary to describe a string. For a perfectly random source, compression will actually increase the length of the string as we'll end up with the original string (the source in this case is its own shortest description) along with the overhead of the compression algorithm. Sounds good, but there's one slight problem – Kolmogorov complexity is an uncomputable function. In the general case, the search space for an ideal compressor is infinite, so while measuring randomness via compressibility kind of works, it's always possible that a compression algorithm exists for which our source is highly compressible, implying that the input isn't so random after all.
What about testing for randomness using the same tools used to assess the quality of a random number generator? NIST offers a test suite for doing so. However, there are several problems with this approach. For starters, these tests need lots of input – 100,000+ data points. Even for high frequency data that makes for a very backward looking measure. Furthermore, the tests are designed for uniformly distributed sample data. We could use the probability integral transform to map our sample from some (potentially empirical) source distribution to the uniform distribution, but now we're stacking assumptions on top of heuristics.
Visualizing Volatility and Entropy
Of the above it sounds like entropy gets us the closest to what we want, so let's see what it looks like compared to volatility. We'll start by plotting the 20 day trailing absolute realized variation of the S&P 500 cash index as a measure of volatility:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
require(quantmod)
require(ggplot2)
require(TTR)
# Calculate open to close log returns on the S&P 500 cash index
sp.data <- dailyReturn(getSymbols("^GSPC", env = .GlobalEnv,
from = "2000-01-01", to = "2013-09-27", src = "yahoo",
auto.assign = FALSE), type = "log")
# Calculate a rolling 20 day absolute realized variation over the returns
sp.arv20 <- tail(runSum(abs(sp.data), n = 20), -19)
sp.arv20.df <- data.frame(
Date = as.Date(index(sp.arv20)),
ARV = as.vector(sp.arv20))
# Plot our results
ggplot(sp.arv20.df, aes(x = Date, y = ARV)) +
geom_line() +
theme(plot.background = element_rect(fill = '#F1F1F1'),
legend.background = element_rect(fill = '#F1F1F1')) +
xlab("Year") +
ylab("Rolling 20 Day Absolute Realized Variation") +
ggtitle("S&P 500 20 Day Absolute Realized Variation vs Time")
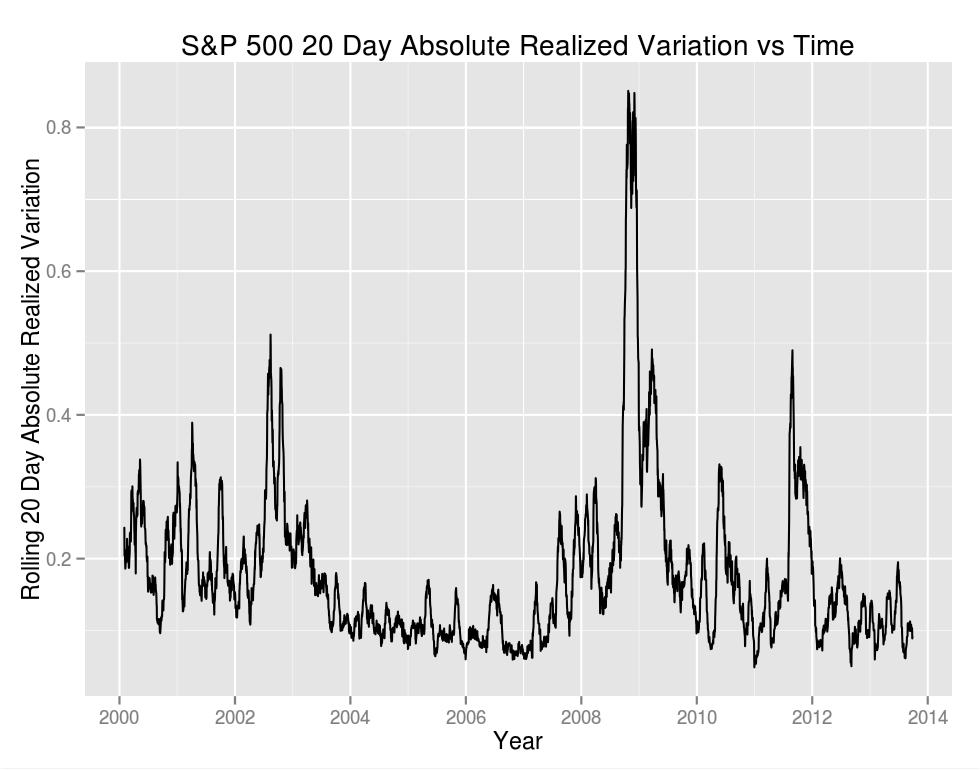
Now let's look at entropy. Entropy is a property of a random variable, and as such there's no way to measure the entropy of data directly. However, if we concern ourselves only with the randomness of up/down moves there's an easy solution. We treat daily returns as Bernoulli trials in which a positive or a zero return is a one and a negative return is a 0. We could use a ternary alphabet in which up, down, and flat are treated separately, but seeing as there were only two flat days in this series doing so only obfuscates the bigger picture.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# Shannon entropy of the Bernoulli distribution
shannon.entropy <- function(x) {
len <- length(x)
p.up <- sum(x >= 0) / len
p.down <- sum(x < 0) / len
total <- 0
if(p.up > 0)
{
total <- total + p.up * log(p.up, 2)
}
if(p.down > 0)
{
total <- total + p.down * log(p.down, 2)
}
return(-total)
}
sp.entropy20 <- tail(rollapply(sp.data, 20, shannon.entropy), -19)
sp.entropy20.df <- data.frame(
Date = as.Date(index(sp.entropy20)),
Entropy = as.vector(sp.entropy20))
ggplot(sp.entropy20.df, aes(x = Date, y = Entropy)) +
geom_line() +
theme(plot.background = element_rect(fill = '#F1F1F1'),
legend.background = element_rect(fill = '#F1F1F1')) +
xlab("Year") +
ylab("Rolling 20 Day Shannon Entropy") +
ggtitle("S&P 500 Rolling 20 Day Shannon Entropy vs Time")
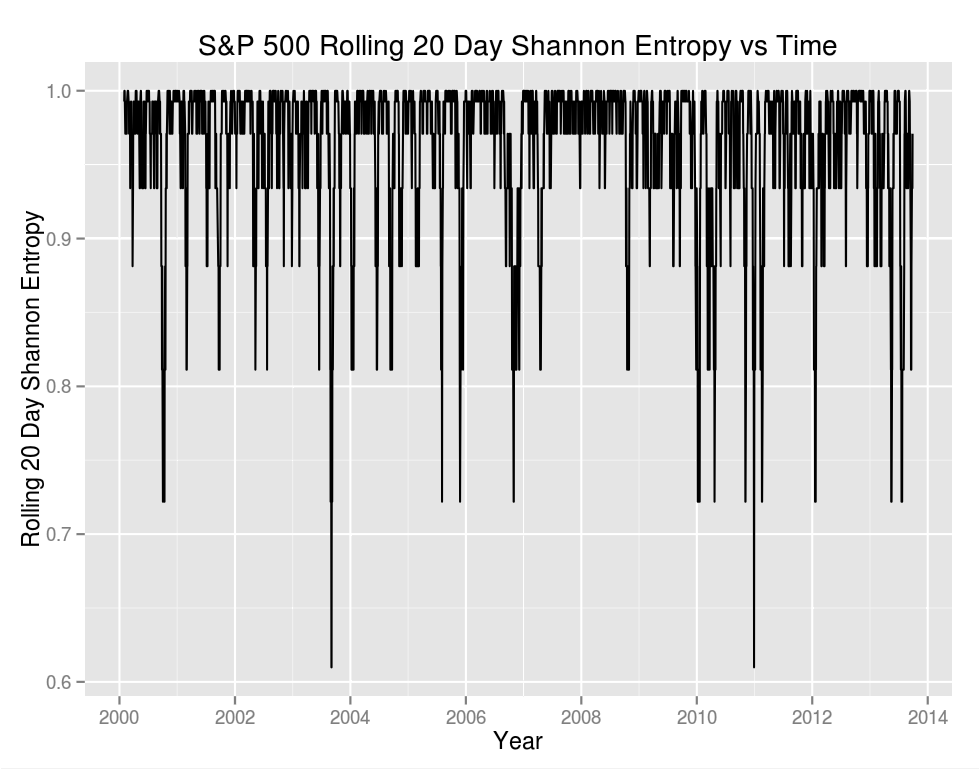
Visually the two plots look very different. We see that most of the time is close to one (the mean is .96), indicating that our "coin" is fair and that the probability of a day being positive or negative over a trailing 20 day period is close to .5.
How correlated are the results? If we consider the series directly we find that . It might be more interesting to consider the frequency in which an increase in volatility is accompanied by an increase in entropy: .500 – spot on random. Entropy and volatility are distinct concepts.
In Closing…
The reoccurring theme of "what are we actually trying to measure," in this case randomness, isn't trivial. Any metric, indicator, or computed value is only as good as the assumptions that went into it. For example, in the frequentist view of probability, a forecaster is "well calibrated" if the true proportion of outcomes is close to the forecasted proportion of outcomes (there's a Bayesian interpretation as well but the frequentist one is more obvious). It's possible to cook up a forecaster that's wrong 100% of the time, but spot on with the overall proportion. That's horrible when you're trying to predict if tomorrow's trading session will be up or down, but terrific if you're only interested in the long term proportion of up and down days. As such, discussing randomness, volatility, entropy, or whatever else may be interesting from an academic standpoint, but profitability is a whole other beast, and measuring something in distribution is inherently backward looking.