Random From Afar but Far From Random
When Random is a Good Thing
The term “random” gets tossed around frequently when describing chaotic processes both physical and artificial. However, true randomness is rare, and a deep enough dive will usually tease out at least some latent structure. Brownian motion enjoys widespread use in academia as a model for “random” processes ranging from molecular diffusion to stock market returns. However, on a small enough scale the laws of quantum mechanics govern diffusion, and exchange microstructure governs the short term price evolution of capital markets.
Randomness plays an integral role in science, mathematics, and technology. High quality random numbers underpin everything from the cryptographic systems that secure e-commerce to Monte Carlo simulations that help us develop pharmaceuticals and predict the weather. Generating truly random numbers can’t be done in software alone as code is inherently deterministic. In order to generate random numbers of cryptographic quality Linux and most operating systems rely on an entropy pool generated by stochastic processes such as disk access and thermal fluctuations. Generating entropy takes time, so instead of consuming from the pool directly the values generated are used to initialize a pseudo random number generator (PRNG) which can in turn produce longer streams of numbers efficiently. Starting with Ivy Bridge, Intel x86 processors provide an instruction to do this in hardware (the RDRAND opcode) but historically heavy users of random numbers relied on userspace code.
PRNG algorithms aim to generate values that appear chaotic and statistically independent. These numbers may exhibit all of the hallmarks of randomness, but the underlying process remains deterministic. Some generators are suitable for cryptographic applications (CSPRNG), and other faster algorithms such as Mersenne Twister are preferred for simulation. Regardless of the algorithm used, subtle flaws and deviations from true randomness may exist in any pseudo random number generator. The RANDU algorithm serves as an infamous example.
Random From Afar but Far From Random
As an early PRNG in the family of Linear Congruential Generators RANDU enjoyed widespread use; it’s fast, easily implemented, and mathematically simplistic. Testing for randomness isn’t an exact science and academic literature focuses largely on heuristics—there’s no definitive method, and with the methods of the time RANDU appeared, well, random.
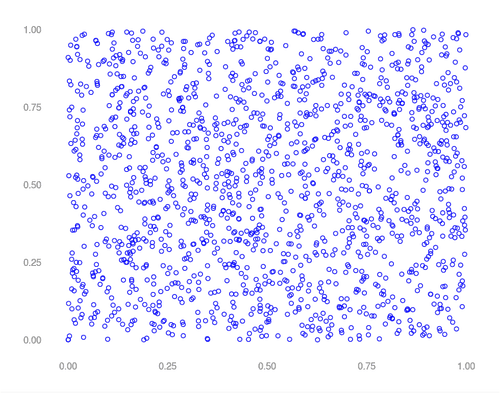
In the image above, successive outputs of RANDU were chosen as (x, y) coordinates. Random, right? What happens if we instead choose successive outputs as (x, y, z) coordinates?

Whoops—clearly not random. Values generated by RANDU fall into 15 two dimensional planes in a three dimensional space —bad news for Monte Carlo. Imagine a simulation generating a random mesh by choosing pseudo random x, y, and z coordinate in succession. RANDU won’t even come close to equally representing all possible coordinates in 3 space. Hindsight being 20/20 the issue with RANDU was purely structural. A simple recurrence relationship exists in which the previous two values returned by the algorithm uniquely determine the next. As every value produced is a linear combination of the last two, numbers produced by RANDU “live” in a structured, three dimensional space. One notes that most PRNGs have this characteristic—just in much higher dimensions where the effects aren’t as obvious or damaging to simulations of physical processes.
Myopic Views
While randomness is a fascinating topic in its own right the profound realization comes from the image above. Viewed in one or two dimensions the flaw in RANDU isn’t obvious; structure only appears under the appropriate transformation to a higher dimensional space. System identification addresses the problem of estimating a state space model (which is itself an n dimensional space where n is the number of states) from noisy, transformed lower dimensional observations. So to what extent can seemingly chaotic data be viewed as a projection down from an orderly high dimensional space? Stay tuned for more on teasing high dimensional structure out of low dimensional data.
