'Tis the Season for September Bearishness?
Is September Bearish?
Traders love discussing seasonality, and September declines in US equity markets are a favorite topic. Historically September has underperformed every other month of the year, offering a mean return of -.56% on the S&P 500 index from 1950 to 2012; 54% of Septembers were bearish over the same period—more than any other month. Empirically, September deserves its moniker: “The Cruelest Month.”
As a trading strategy 54% isn’t a substantial win rate, and small N given that it only trades once a year. However, both as a portfolio overlay and as a trading position it’s worth considering whether bearishness in September is a statistically significant anomaly or random noise.
Issues With Testing for Seasonality
There are plenty of tests for seasonality in time series data. Many rely on some form of autocorrelation to detect seasonal components in the underlying series. These methods are usually parametric and subject to lots of assumptions— not robust, especially for a non-stationary, noisy time series like the market.
Furthermore, sorting monthly returns by performance and declaring one month “the most bearish” introduces a data snoop bias. We’re implicitly performing multiple hypothesis tests by doing so, and as such we need to correct for the problem of multiple comparisons. This gets even more interesting if we consider a spreading strategy between two months, which introduces a multiple comparison bias closely related to the Birthday Paradox.
Bootstrap to the Rescue
The non-parametric bootstrap is a general purpose tool for estimating the sampling distribution of a statistic from the data itself. The technique is a powerful, computationally intensive tool that’s easily applied for any sample statistic, works well on small samples, and makes few assumptions about the underlying data. However, one assumption that it does make is a biggie: the data must be independent, identically distributed (iid). That’s a deal breaker, unless you buy into the efficient market hypothesis, in which case this post is already pretty irrelevant to you. Bootstrapping dependent data is an active area of research and there’s no universal solution to the problem. However, there’s research showing that the bootstrap is still robust when these assumptions are violated.
To address the question of seasonality we need a reasonable way to pose the hypothesis that we’re testing—one that minimizes issues arising from path dependence. One approach is to consider the distribution of labeled and unlabeled monthly returns. This flavor of bootstrap is also known as a permutation test. The premise is simple. Data is labeled as “control” and “experimental.” Under the null hypothesis that there’s no difference between two groups a distribution is bootstapped over unlabeled data. A sample mean is calculated for the experimental data, and a p-value is computed by finding the percentage of bootstrap replicates more extreme than the sample mean. September returns form the experimental group, and all other months comprise the control.
The Study
The monthly (log) return was calculated using the opening price on the first trading day of the month and the closing price on the last trading day. Adjusted returns on the S&P index were used in lieu of e-minis or SPY in the interest of a longer return series (we’re interested in the effect, not the execution, and on the monthly level there won’t be much of a difference in mean).
We’ll start by taking a look at the bootstrapped distributions of mean monthly returns. The heavy lifting is done by the fantastic XTS, ggplot, and quantmod libraries.
require(quantmod)
require(boot)
require(ggplot2)
require(reshape2)
require(plyr)
# Download OHLCV data for the S&P 500 cash index
sp.data <- getSymbols("^GSPC", env = .GlobalEnv, from = "1950-01-01",
to = "2012-12-31", src = "yahoo", auto.assign = FALSE)
# Calculate the adjusted monthly log return
sp.adj.close <- sp.data[, 6]
sp.monthly.ret <- to.monthly(sp.adj.close, drop.time = TRUE,
indexAt = 'yearmon')
sp.monthly.ret <- log(sp.monthly.ret[, 4] / sp.monthly.ret[, 1])
# Split the data into returns, grouped by month
by.month <-split(sp.monthly.ret, .indexmon(sp.monthly.ret))
bootstrap.groups <- c(sapply(by.month, function(x) {
format(index(first(x)), "%B") }), "Control")
bootstrap.groups <- factor(bootstrap.groups, levels = bootstrap.groups)
# Bootstrap replicate sample count
sample.count <- 10000
# A function to bootstrap the emperical distribution of the sample mean
boot.fun <- function(df) {
samplemean <- function(x, index) { return(mean(as.vector(x)[index])) }
boot(data = df, statistic = samplemean, R = sample.count)$t
}
# Calculate a bootstrap distribution for returns data drawn from each month,
# and a control group containing unlabeled data from all months.
boot.results <- lapply(by.month, boot.fun)
boot.results[[length(boot.results) + 1]] <- boot.fun(sp.monthly.ret)
names(boot.results) <- bootstrap.groups
df <- melt(as.data.frame(boot.results))
names(df) <- c("Month", "Return")
# Calculate the mean return for each month and the control
mean.returns <- ddply(df, .(Month), summarise, Return = mean(Return))
# Sort the bootstrap means for the ggplot legend
return.order <- with(mean.returns, order(Return))
mean.returns <- mean.returns[return.order, ]
df <- df[with(df, order(match(Month, mean.returns$Month))), ]
# Reset the levels so that our plot legend displays in the order that we want
df$Month <- factor(df$Month,
levels = levels(mean.returns$Month)[return.order])
# Build legend labels (ggplot handles the rendering of special symbols using
# bquotes)
legend.labels <- mapply(
function(month, ret) {
bquote(paste(.(as.character(month)), ": ",
mu == .(round(as.numeric(ret), 4)), sep = ""))
},
mean.returns$Month,
mean.returns$Return
)
# Draw a density plot of the bootstrap distributions and the control
ggplot(df, aes(x = Return, fill = Month)) +
geom_density(alpha = .3) +
scale_fill_discrete(labels = legend.labels) +
theme(plot.background = element_rect(fill = '#F1F1F1'),
legend.background = element_rect(fill = '#F1F1F1')) +
ylab("Bootstrapped Frequency") +
ggtitle("Bootstrapped Returns By Month")
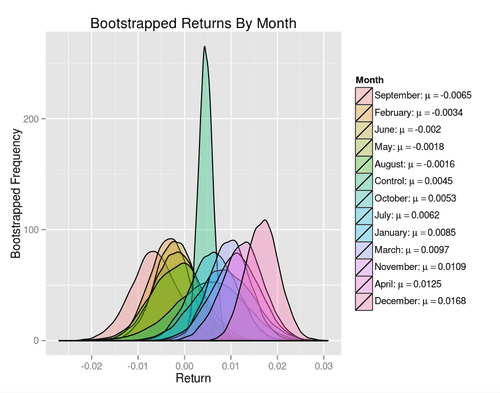
The image above shows a bootstrap distribution for each calendar month, as well as the control. The control distribution is much tighter as there’s 12 times more data, which by the Central Limit Theorem should result in a distribution having .
Plots of boostrapped distributions offer a nice visual representation of the probability of committing type I and type II errors when hypothesis testing. The tail of the single month return distributions extending towards the mean of the control distribution shows how a Type II error can occur if the alternative hypothesis was indeed true. The converse holds for a Type I error in which the tail of the null hypothesis distribution extends towards the mean of an alternative hypothesis distribution.
Now for the permutation test.
# Split our monthly returns into a September and a "Not September" group
sep.returns <- as.vector(sp.monthly.ret[.indexmon(sp.monthly.ret) == 7, ])
ex.sep.returns <- unlist(split(sp.monthly.ret[
.indexmon(sp.monthly.ret) != 7, ], f = "years"))
# Compute the mean difference between the group
mean.diff.sep <- mean(ex.sep.returns) - mean(sep.returns)
# Pool the two groups and create sample.count bootstrap replicates
pooled <- c(sep.returns, ex.sep.returns)
sample.mat <- matrix(data = pooled, nrow = sample.count,
ncol = length(pooled), byrow = TRUE)
sampled <- t(apply(sample.mat, 1, sample))
group1 <- sampled[, 1:length(sep.returns)]
group2 <- sampled[, (length(sep.returns) + 1):length(pooled)]
# Compute the mean difference between our two permuted sample groups
mean.diff.sampled <- data.frame(mean.diff =
apply(group1, 1, mean) - apply(group2, 1, mean))
# Plot a distribution of mean differences between monthly returns
mean.diff.df <- data.frame(Means = c("Permuted", "September"),
Value = c(mean(mean.diff.sampled), mean.diff.sep))
ggplot(mean.diff.sampled, aes(x = mean.diff)) +
geom_histogram(aes(y = ..density..), colour = "black", fill = "white") +
geom_density(alpha = .3, fill = "#66FF66") +
geom_vline(data = mean.diff.df,
aes(xintercept = Value,
linetype = Means,
colour = Means),
show_guide = TRUE) +
theme(plot.background = element_rect(fill = '#F1F1F1'),
legend.background = element_rect(fill = '#F1F1F1')) +
xlab("Difference Between Monthly Returns") +
ylab("Bootstrapped Frequency") +
ggtitle("Sample Permutation Distribution of Differences in Monthly Returns")
cat(sprintf("p-value: %.4f\n",
sum(mean.diff.sampled > mean.diff.sep) / sample.count))
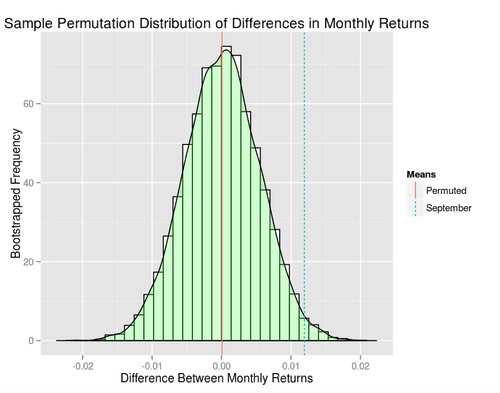
My p-value was (your mileage will vary as this a random sample after all)—pretty statistically significant as a stand alone hypothesis. However, we still have a lurking issue with multiple comparisons. We cherry picked one month out of the calendar year—September—and we need to account for this bias. The Bonferroni correction is one approach, in which case we would need if we were testing our hypothesis at the level. Less formally our p-value is effectively 0.1608—not super compelling.
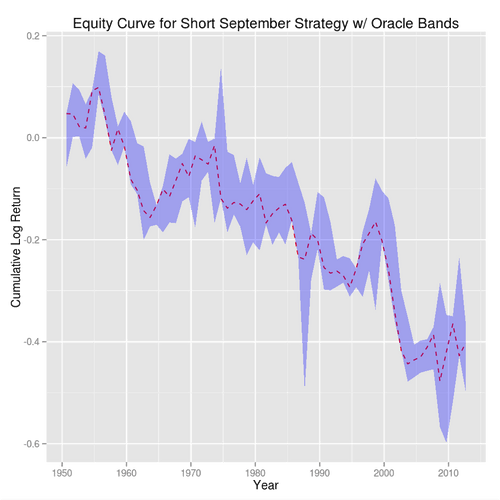
Putting the statistics aside had you traded this strategy from 1950 to present your equity curve (in log returns) would look like:
sep.return <- sp.monthly.ret[.indexmon(sp.monthly.ret) == 7, ]
sep.return.vals <- as.vector(sep.return)
sep.return.cum <- cumsum(sep.return.vals)
sep.return.cum.delta <- sep.return.cum - sep.return.vals
high.band <- sep.return.cum.delta + sapply(split(
sp.monthly.ret, f = "years"), max)
low.band <- sep.return.cum.delta + sapply(split(
sp.monthly.ret, f = "years"), min)
return.bands <- data.frame(
Date = as.Date(index(sep.return)),
Return = sep.return.cum,
High = high.band,
Low = low.band)
ggplot(return.bands, aes(x = Date, y = Return, ymin = Low, ymax = High)) +
geom_line(color = 'red', linetype = 'dashed') +
geom_ribbon(fill = 'blue', alpha = .3) +
theme(plot.background = element_rect(fill = '#F1F1F1'),
legend.background = element_rect(fill = '#F1F1F1')) +
xlab("Year") +
ylab("Cumulative Log Return") +
ggtitle("Equity Curve for Short September Strategy w/ Oracle Bands")
The high and low bands show the return for the most bullish and bearish month in each year. It’s easy to see that September tends to hug the bottom band but it looks pretty dodgy as a trade—statistical significance does not a good trading strategy make.
Closing Thoughts
Bootstrapping September returns in aggregate makes the assumption that year-over-year, September returns are independent, identically distributed. Given that the bearishness of September is common lore, it’s reasonable to hypothesize that at this point the effect is a self-fulfilling prophecy in which traders take into account how the previous few Septembers went, or the effect in general. If traders fear that September is bearish and tighten stops or liquidate intra-month, an anomaly born out random variance might gain traction. Whatever the cause, the data indicates that September is indeed anomalous. As for a stand-alone trading strategy…not so much.
